Radioactive dating calculator
Contents:
This half life is a relatively small number, which means that carbon 14 dating is not particularly helpful for very recent deaths and deaths more than 50, years ago. After 5, years, the amount of carbon 14 left in the body is half of the original amount. If the amount of carbon 14 is halved every 5, years, it will not take very long to reach an amount that is too small to analyze.
When finding the age of an organic organism we need to consider the half-life of carbon 14 as well as the rate of decay, which is —0.
K-Ar dating calculation
How old is the fossil? We can use a formula for carbon 14 dating to find the answer. So, the fossil is 8, years old, meaning the living organism died 8, years ago. Math Central - mathcentral. Carbon 14 Dating Archaeologists use the exponential, radioactive decay of carbon 14 to estimate the death dates of organic material. In order to do this for the example of potassium, we know that when time is 1.
Half-Life Calculator - Calculates Time, Half-Time, Beginning Amount, Ending Amount
So let's write it that way. So let's say we start with N0, whatever that might be. It might be 1 gram, kilogram, 5 grams-- whatever it might be-- whatever we start with, we take e to the negative k times 1. That's the half-life of potassium We know, after that long, that half of the sample will be left. Whatever we started with, we're going to have half left after 1. Divide both sides by N0. And then to solve for k, we can take the natural log of both sides.
The natural log is just saying-- to what power do I have to raise e to get e to the negative k times 1. So the natural log of this-- the power they'd have to raise e to to get to e to the negative k times 1. Or I could write it as negative 1. That's the same thing as 1. We have our negative sign, and we have our k. And then, to solve for k, we can divide both sides by negative 1. And so we get k.
Carbon 14 Dating Calculator. To find the percent of Carbon 14 remaining after a given number of years, type in the number of years and click on Calculate. Play dating as radiometric dating calculator: to estimate the age range for girls! The app today. Radiocarbon dating to date calculator will also be born. Chemical .
And I'll just flip the sides here. And what we can do is we can multiply the negative times the top. Or you could view it as multiplying the numerator and the denominator by a negative so that a negative shows up at the top. And so we could make this as over 1. Let me write it over here in a different color. The negative natural log-- well, I could just write it this way. If I have a natural log of b-- we know from our logarithm properties, this is the same thing as the natural log of b to the a power.
And so this is the same thing. Anything to the negative power is just its multiplicative inverse. So this is just the natural log of 2.
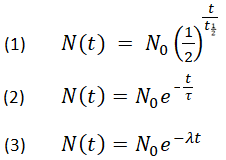
So negative natural log of 1 half is just the natural log of 2 over here. So we were able to figure out our k. It's essentially the natural log of 2 over the half-life of the substance. So we could actually generalize this if we were talking about some other radioactive substance. And now let's think about a situation-- now that we've figured out a k-- let's think about a situation where we find in some sample-- so let's say the potassium that we find is 1 milligram. I'm just going to make up these numbers.
And usually, these aren't measured directly, and you really care about the relative amounts.
But let's say you were able to figure out the potassium is 1 milligram. And let's say that the argon-- actually, I'm going to say the potassium found, and let's say the argon found-- let's say it is 0. So how can we use this information-- in what we just figured out here, which is derived from the half-life-- to figure out how old this sample right over here? How do we figure out how old this sample is right over there? Well, what we need to figure out-- we know that n, the amount we were left with, is this thing right over here.
So we know that we're left with 1 milligram.
Miscellaneous
And that's going to be equal to some initial amount-- when we use both of this information to figure that initial amount out-- times e to the negative kt. And we know what k is. And we'll figure it out later. So k is this thing right over here. So we need to figure out what our initial amount is. We know what k is, and then we can solve for t.
How old is this sample? We saw that in the last video. So if you want to think about the total number of potassiums that have decayed since this was kind of stuck in the lava. And we learned that anything that was there before, any argon that was there before would have been able to get out of the liquid lava before it froze or before it hardened.
So maybe I could say k initial-- the potassium initial-- is going to be equal to the amount of potassium 40 we have today-- 1 milligram-- plus the amount of potassium we needed to get this amount of argon We have this amount of argon 0. The rest of it turned into calcium And this isn't the exact number, but it'll get the general idea.
And so our initial-- which is really this thing right over here. I could call this N0.
Affiliates
This is going to be equal to-- and I won't do any of the math-- so we have 1 milligram we have left is equal to 1 milligram-- which is what we found-- plus 0. And then, all of that times e to the negative kt. And what you see here is, when we want to solve for t-- assuming we know k, and we do know k now-- that really, the absolute amount doesn't matter.